Toy Computing. Unkonventionelle Verfahren spielerischer Informatik-(Selbst-)Ausbildung
Einleitung
Alternative Computer-Konzepte, wie Computing mit Pflanzen, mit Flüssigkeiten, Analogcomputing, Collision Based Computing (und ähnliche Ansätze des so genannten Unconventional Computing1) zeigen nicht nur neue Möglichkeiten in der Entwicklung von Computertechnologie; sie sind auch durch ihre Andersartigkeit geeignet, auf längst als selbstverständlich akzeptierte Konzepte aus einer alternativen Perspektive hinzuweisen und zu (hinter-)fragen, wie sich spezifische Elemente des Computers und des Computings (den Tätigkeiten von Computern) so und nicht anders entwickelt haben, wie sie heute vorliegen. Die Computerarchäologie2 versucht solche ‚epistemologischen Revisionen‘ theoretisch zu reflektieren und an praktischen Beispielen zu erproben. Hierbei nehmen unkonventionelle Computing-Verfahren eine besondere Stellung ein, weil an ihnen spezifische/einzelne Elemente des Computing akzentuiert werden und damit von emergent-komplexen Informatik-Systemen (Computern) abstrahieren.
Eine solche Hands-on-Epistemologie ließe sich im akademisch-experimentellen Sinne als ‚spielerisches T(h)inkering’3 bezeichnen. Hierfür eignen sich besonders komputierende Spielzeuge, denn in ihnen liegen Funktionen oft in vergrößerter Reinform vor, um die Funktionalität spezifischer Elemente (im folgenden: des Computers und des Computing) im Sinne einer spielerischen Didaktik begreifbar zu machen. Die Überlegungen des folgenden Beitrags basieren auf diesem mittlerweile siebzig Jahre alten Konzept, das hier als ‚Toy Computing‘ definiert wird: die Nutzung oder Umwidmung von Spielzeugen zum Zwecke des Computing und der ‚Rechnerkunde‘4. Nach einem kurzen historischen Überblick über Computing Toys, in dessen Zuge verschiedene materielle und dann virtuelle ‚Vorstufen‘ von Minecraft vorgestellt werden, werden einige Grundlagen des Schaltungsentwurfs in Minecraft dokumentiert und das Konzept theoretisch innerhalb des Unconventional Computing verortet. Im Anschluss führt eine Anwendungsfall vor, wie die Implementierung von Digitaltechnologie mit/in Minecraft spielerisch vollzogen werden kann.5
Der didaktische Ansatz basiert auf dem Konzept des Blended Learning, bei dem unterschiedliche Lehr-/Lernmethoden zum Einsatz kommen: theoretische Grundlagenvermittlung im Frontalunterricht (Aussagenlogik, Boole‘sche Algebra, Basisschaltungen digitaler Medien), gemeinsame Projektentwicklung im Präsenzdialog zwischen den Seminarteilnehmer:innen und dem Seminarleiter sowie autodidaktische Projektumsetzung im Learning-by-doing- und Trial-and-Error-Verfahren. In allen Stadien der Projektvorbereitung und -vermittlung wurden sowohl konventionelle Quellen6 als auch Online-Datenbanken (Planet Minecraft7, Minecraft Wiki8) und Lehrvideos (YouTube) eingesetzt. Nach der Grundlagenvermittlung erfolgte die Erarbeitung von Projekten auf Basis dieser Quellen im deduktiven Verfahren: Fertige fremde Konstrukte wurden auf ihre konventionellen und unkonventionellen Technologien hin analysiert und Elemente daraus nachgebaut. Auf diese Weise wurde das Konzept ‚Toy Computing‘ an Minecraft als epistemischem Spiel(-zeug) entwickelt und weiterentwickelt.
Die Quellen, die als Informationsgrundlage dienten, sind frei zugänglich; das Spiel Minecraft kann für zahlreiche Computerplattformen kostengünstig erworben werden. Dieser niederschwellige Zugang garantiert die Möglichkeit, die beschriebenen Verfahren auch autodidaktisch zu erarbeiten – ein modus operandi, der aus der Hacker- und Maker-Kultur der zweiten Hälfte des 20. Jahrhunderts stammt und bis heute in technik-hobbyistischen Subkulturen gelebt wird. Getrieben werden solche autodidaktischen Annäherungen an Computer- und Digitaltechnologie durch den Wunsch der Selbstermächtigung der User über das Device, das ihnen nicht länger als bloßes Werkzeug zum Erledigen von Arbeiten dienen soll, sondern selbst zum „Zeug“9 wird, das es zu erforschen gilt, um Souveränität darüber zu erlangen. Dieser Prozess vollzieht sich in einer Art von ‚eLearning‘, bei dem die (selbe) Technologie „zuerst als Lehrgegenstand, den der Leser kennen lernen soll, und dann als Lehrgegenstand, den er lehren lernen soll“10. Der Computer selbst tritt dabei sowohl als Dialogpartner im ‚Trial and Error‘-Prozess auf als auch als Werkstück, das es zu bearbeiten gilt. Mit fortschreitendem Verständnis der Computingprozesse erlangen die User Souveränität über ihre Geräte.
Geschichte des Toy Computing
Toy Computing beschreibt hier11) die Nutzung und Umnutzung von Spielzeugen zu komputativen Zwecken. Vor diesem Hintergrund lassen sich bereits Georg Wilhelm Leibniz' 1679 konzipierte Machina Aritmethica Dyadica12 unter diesem Begriff fassen: Mit ihnen können Dualzahlen dargestellt und addiert werden, indem Kugeln/Murmeln auf einer schiefen Bahn in leere Mulden (binär: 0) versenkt werden. Dort, wo sich bereits eine Kugel in einer Mulde befindet (binär: 1) führt das Einfüllen einer weiteren Kugel zur Leerung und zum Übertrag der Kugel in die Mulde der nächsten leeren Dualstelle (vgl. Abb. 1). Das Prinzip dieser einfachen Rechenmaschine basiert auf einer Art von Collision Based Computing13 und findet seine ‚dezimale‘ Entsprechung in den Kugelrechenmaschinen und Abakussen, die bereits im dritten Jahrtausend vor unserer Zeitrechnung als Rechenhilfsmittel benutzt werden.

Abbildung 1: Machina Aritmethica Dyadica (Leibniz, 1679 – Nachbau des Deutschen Technikmuseums, Berlin)
In den 1960er-Jahren entwickelte die Firma Education Science Research Inc. (E.S.R.) Spielzeuge mit (informatik-)didaktischem Anspruch, die ebenfalls mit Kugeln operieren. Zu nennen wären hier das Spiel The Amazing Dr. Nim (1966) sowie der Digi-Comp II (1967)14. Ersteres stellt eine NIM-KI15 dar, die mithilfe dreier mechanischer Flip-Flops, eines Equalizers und 15 Murmeln16 einen künstlichen Spieler implementiert, der gegen eine:n menschliche:n Opponenten:in das NIM-Spiel spielt.17 Der informatikdidaktische Anspruch des Spiels wird in dessen Manual expliziert: Nach einer Einführung in die Boole‘sche Algebra (6-11), erfährt der/die Spieler:in, wie man Dr. NIM spielend programmiert (12-15) und erhält abschließend eine Einordnung des Spielcomputers in die Domäne der Künstlichen Intelligenz (15-20).
Digi-Comp II stellt bereits einen Computer dar, welcher Berechnungen der Komplexitätsklasse zwischen NL und P lösen kann.18 Er basiert ebenfalls auf einem System aus mechanischen Flip-Flops (organisiert in einem 4-Bit-Speicher, einem 7-Bit-Akkumulator sowie einem 3-Bit-Multiplizier-Register) einem Dateneingang (‚Input Guide‘), durch welchen die Murmeln als Eingangssignale von oben nach unten laufen, und einem Datenausgang (‚Collector Guide‘), in welchem sie als Ergebnis abgelegt werden. Für die Programmierung von Digi-Comp II wird im Manual eine Maschinensprache und die ‚höhere‘ Compiler-Sprache „Digi-Tran“ (14) vorgestellt. Wie bei Dr. NIM steht auch hier die informatikdidaktische Intention im Vordergrund:
DIGI-COMP II is an educational computer which actually works in a manner analogous to an electronic digital computer. (…) The various operations that DIGI-COMP II performs are executed in slow motion as compared with an electronic machine. (…) This enables the person operating DIGI-COMP II to comprehend what is happening as it occurs.19
Digi-Comp II wurde 2012 nachgebaut. Es existieren noch eine Reihe weiterer kugelbasierter Spielzeug-Computer; die logische Grundstruktur von Rechenmaschinen lässt sich auf vielfältige Weise mit Spielzeug konstruieren.20 Eine der jüngsten Implementierungen heißt Turing Tumble (2012): Ein Spiel aus verschiedenen mechanischen Schalt- und Regelelementen, mit dem sich ein turingvollständiges Computersystem21 implementieren lässt. (Vgl. Abb. 2) „Mit einer turingvollständigen oder turingmächtigen Sprache lassen sich alle Funktionen einer universellen Turingmaschine bzw. einer konkreten Computerhardware aufrufen. Die enthält insbesondere Funktionen für die Programmierung von Schleifen und für bedingte Programmverzweigungen.“22. <https://paidia.de/computerspiele-computerspiele-referenzen-zitate-und-rekursionen-des-computers-als-spiel/> [06.06.2025], siehe auch Fußnote 36.))

Abbildung 2: Dr. NIM, Digi-Comp II, Turing Tumble
Neben solchen Rechensystemen, die auf physikalischer Kollision und Ablenkung von Kugeln basieren, existieren auch virtuelle Spielsysteme, die auf dem Kollisionsprinzip basieren. Zu den bekanntesten zählen die zellulären Automaten – und allen voran Conway‘s Game of Life.23 Prinzipiell lassen sich viele Spielalgorithmen als Zellularautomaten interpretieren und darstellen. Hierzu müssen diskrete Zustände einzelner Zellen existieren, die sich regelbasiert ändern. Die Anzahl und Komplexität der Regeln, die Anzahl unterschiedlicher Zellen und Zellzustände sowie die Frequenz der Taktung können dabei stark variieren. Vor diesem Hintergrund lässt sich auch das Spiel Minecraft als zellulärer Automat beschreiben – und wie beispielsweise im Game of Life24 ist es auch bei Minecraft25 möglich turingvollständige Computersimulationen innerhalb des Spiels zu generieren. Dies soll im Folgenden exemplarisch durch die Implementierung eines NAND-Gatters26 in Minecraft belegt werden.
Digitale Logik in Minecraft
Das Computerspiel Minecraft wurde 2009 von der Firma Mojang entwickelt und bis heute für unterschiedliche Plattformen publiziert. 2014 wurde es durch Microsoft aufgekauft. Bei Minecraft handelt es sich um ein Open-World-Spiel mit Adventure- und Role-Play-Gaming-Elementen. Es kann im Einzel- oder Mehrspielermodus offline oder im Netzwerk gespielt werden. In den Spielmodi ‚Überleben‘, ‚Adventure‘ und ‚Hardcore‘ müssen sich die Spielenden aus basalen Materialien, die aus der Spielwelt abgebaut (‚mining‘) werden, komplexere Gegenstände konstruieren (‚crafting‘). Dies reicht von Baublöcken über Lebensmittel, Waffen und Werkzeugen bis hin zu Zaubertränken, Schildrüstungen und sogar Lebewesen. Im ‚Kreativmodus‘ sind fast alle möglichen Gegenstände für den Spieler in beliebiger Anzahl frei verfügbar. Der Kreativmodus ermöglicht damit insbesondere das gestalterische und experimentelle Spielen mit den funktional unterschiedlichen Blöcken und Spielgegenständen.
Seit 2013 verfügt das Spiel über ‚Redstones‘. Dabei handelt es sich um Spielblöcke, die Signale übertragen und verarbeiten können. In den Nicht-Kreativmodi muss das Redstone-Erz zunächst in ausreichender Menge abgebaut (‚mining‘) werden, um daraus anschließend Redstone-Objekte zu konstruieren (‚craften‘). Im Kreativmodus sind alle diese Redstone-Objekte bereits vorhanden. Hierzu zählen neben den Redstone-Blöcken verschiedene Schalter, Taster, Lampen, Klappen und Türen, Verstärker und Komparatoren, die den Signalfluss regeln, steuern, als Signalquellen und -senken dienen. Die Redstone-Technologie hat ein großes Echo in der Minecraft-Community hervorgerufen. In dessen Rahmen sind zahlreiche Maschinenimplementierungen entwickelt worden, die von einfachen Schaltsystemen (wie zum Beispiel Aufzügen) bis hin zu Schaltkreisen, CPUs und funktionsfähigen Computer- und Computerspielsystemen reichen. Aufgrund dieser Verwendungsmöglichkeiten hat Microsoft 2016 eine Education Minecraft Plattform27 initiiert und das Spiel bereits Eingang in die Hochschul- und Schulinformatik gefunden.28
Signalerzeugung und -transport
Mit der Redstone-Technologie ist es möglich, innerhalb der virtuellen Spielwelt von Minecraft Signalübertragungs- und -verarbeitungsapparaturen zu konstruieren. Redstone dient hierbei sowohl als Signalträger als auch als Signalleiter: Eine Spur aus Redstone-Staub, aufgebracht auf ein Substrat29, fungiert als Signalleitung; der Signaltransport kann aktiviert werden, wenn eine Fackel, ein Taster, ein Hebel oder eine Druckplatte an die Spur angebaut und betätigt werden. Als Signalsenke kann beispielsweise eine Redstone-Lampe fungieren, die zu leuchten beginnt, sobald sie über die Redstone-Leitung ein Signal erhält. Die Signalreichweite ist dabei nicht unbegrenzt: Gleich einem Leitungswiderstand wird das Signal mit der Entfernung von der Quelle schwächer. Dies kann durch Einbringen eines Verstärkers kompensiert werden. Ebenso findet der Signaltransport verzögert statt; je nach Leitungslänge können hierbei bemerkbare Latenzen entstehen, was insbesondere bei der Synchronisation taktgesteuerter Digitalbausteine zu berücksichtigen ist. Neben der Redstone-Technologie existieren noch (quasi-)mechanische Schaltverfahren, die mithilfe von Trichtern (Hopper30), Kolben (Piston31) oder Loren (Minecart32) fungieren. Diese – gleichwohl ebenso unkonventionellen – Verfahren werden hier nicht näher beschreiben.
NAND-Gatter
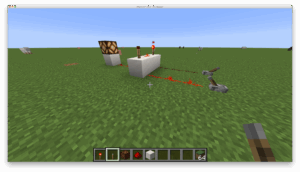
Es gibt verschiedene Möglichkeiten ein NAND-Gatter mittels Redstone-Technologie zu implementieren. Intuitiv kann man sich dabei an der herkömmlichen Schaltungslogik orientieren und ein AND-Gatter mit negiertem Ausgang konstruieren (Abb. 3). Allerdings zeigt sich hierbei bereits ein Unterschied zwischen Redstone- und elektrischen Signalen: Der Signaltransport scheint mehrfach unterbrochen zu sein: Vom linken und vom rechten Schalthebel läuft je ein Signal auf den linken und den rechten Block zu, auf dem sich je eine Fackel befindet. Die Fackeln sind miteinander über den mittleren Block durch Redstone verbunden. Vorn am mittleren Block befindet sich eine dritte Fackel. Von dort aus läuft das Redstone-Signal zur Senke (einer Redstone-Lampe):
| Input l | Input r | Fackel l | Fackel r | Fackel m | Output |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 |
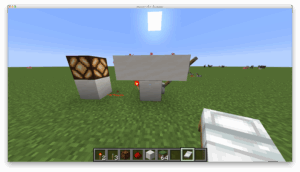
Die linke Fackel indiziert damit eine Negation des linken Inputs, die rechte eine Negation des rechten Inputs. Die mittlere Fackel bildet die Disjunktion beider Inputs beziehungsweise die Sheffer-Funktion der linken und rechten Fackel. Sie negiert schließlich das Ausgangssignal für den Output. Die scheinbare ‚Unterbrechung‘ unterstreicht den Charakter des zellulären Automaten, denn nicht die visuelle Verbindung der grafischen Elemente, sondern die Nachbarschaft der funktionalen Blöcke garantieren die Konnektivität. Dies zeigt sich besonders deutlich in der vertikalen und der adjenkten Bauweise des NAND-Gate: Bei ersterer überträgt die Fackel des oberen Eingangs das Schaltsignal scheinbar über die Luft zur Senke, bei letzterer schwebt ein funktionales Element scheinbar isoliert von der Schaltung in der Luft.
 |
 |
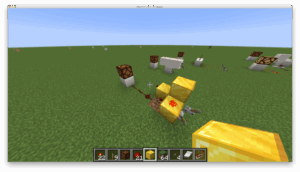 |
Abbildung 3: NAND-Gatter in Redstone-Technik in Standard- (Links), vertikaler (Mitte) und kompakter/adjenkter Bauweise (Rechts)
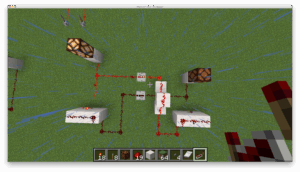
Diese unterschiedlichen Konstruktionsmöglichkeiten von Gattern und anderen digitalen Bauelementen erlauben vergleichsweise kompakte Schaltnetze. Dies zeigt der abschließende Vergleich eines RS-Flip-Flops, das (Abb. 4, links) in konventioneller und (Abb. 4, rechts) kompakter Bauweise realisiert wurde. Die Unterschiede lassen sich im Platzbedarf und im ‚Verbrauch‘ von Konstruktionsblöcken quantifizieren:
| RS-Flip-Flop | Inputs | Redstone | Bauelemente | Fackeln | Verstärker | Outputs |
| Konventionell | 2 | 30 | 11 | 2 | 2 | 2 |
| Kompakt | 2 | 13 | 4 | 2 | 0 | 2 |
Abbildung 4: RS-Flip-Flop in konventioneller (links) und kompakter (rechts) Bauweise
 |
 |
Für die konventionelle Bauweise mit zwei NAND-Gattern werden mehr als doppelt so viele Bauelemente (unter anderem, um zwei Leitungen voneinander zu isolieren) und Redstone-Elemente (unter anderem Verstärker, die den Signalverlust auf den sehr langen Leitungen kompensieren) benötigt.
Digitale Schaltkreise in Minecraft und das Erbe der Elektronik
Eine mögliche Anwendung digitaler Systeme sind Schaltkreise, mit denen arithmetische Aufgaben gelöst werden können. Die Addition dualer Zahlen spielt eine entscheidende Rolle in der Digitaltechnologie, weil alle anderen grundlegenden arithmetischen Operationen aus der Dualzahlenaddition abgeleitet werden. Der Schaltkreis, der eine solche Addition durchführt, kann leicht mit Hilfe von Logik-Schaltgattern realisiert werden – in Hardware zum Beispiel mit Hilfe eines Transistor-Transistor-Logik-Schaltkreises (TTL). Da durch Einsatz der Redstone-Technologie in Minecraft Logikgatter, wie oben gezeigt, nachgebildet werden können, ist es auch möglich, einen Schaltkreis zu implementieren, der eine solche arithmetische Aufgabe lösen kann. Selbstverständlich zeigen sich dabei Unterschiede zu einer funktionsgleichen elektronischen Schaltung; allerdings finden sich auch Ähnlichkeiten, die Aufschluss über die Technologie geben können. Das Ziel des folgenden Experimentes ist es, die Unterschiede und Ähnlichkeiten von Digitaltechnik-Implementierungen in TTL und Redstone-Technologie anhand eines so genannten Halbaddierers zu ergründen. Bevor wir die Implementierung in Minecraft darstellen, muss die konventionelle Darstellung in digitaler Elektronik erfolgen. So zeigen sich die Ähnlichkeiten und Unterschiede beider, aus der die didaktische Vorteile der Simulation hervorgehen.
Der Schaltkreis
Die Addition zweier Dualzahlen kann mit Hilfe zweier logische Gatter realisiert werden. Durch das Verbinden eines XOR- und eines AND-Gatter lässt sich ein Halbaddierer konstruieren. Dieser stellt eine Standardschaltung der Digitaltechnologie dar, besitzt allerdings einen entscheidenden Nachteil: Mit ihm können nur zwei einstellige Dualziffern zu einer Summe und einem Übertrag addiert werden. Größere Dualzahlen bedürfen zur Addition eines Volladdierers, der aus zwei Halbaddierern besteht (Abb. 5). Zusätzlich zu den zwei Eingängen (Input 1 und Input 2) besitzt dieser Volladdierer noch einen weiteren Eingang für das Übertragssignal, das aus der vorherigen Addition stammt (Carry in).
Abbildung 5: Volladdierer aus zwei Halbaddierern in Logisim
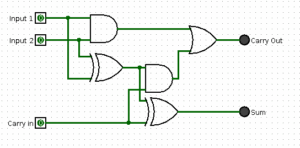
Mit Hilfe der Schaltung aus Abb. 5 können zwei Dualziffern (eingegeben über die Eingänge Input 1 und Input 2) miteinander addiert werden. Um die Anzahl der Binärziffern zu vergrößern (also größere Zahlen miteinander zu addieren) und das Übertragsbit für Vergleiche nutzen zu können, wird ein weiterer Volladdierer angeschlossen. Der Übertrags-Ausgang des ersten Volladdierers wird dann mit dem Übertragseingang des zweiten verbunden. Auf diese Weise können 4 Dualziffern (4 Bit) mit dem in Abb. 6 gezeigten Addierwerk aufsummiert werden.
Abbildung 6: 4-Bit-Volladdierer simuliert mit Logisim (mit einem aktiven Input)
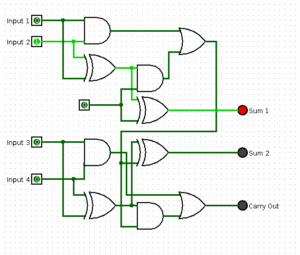
Ein 4-Bit-Volladdierer mit TTL-Logik
Für komplexere Schaltungen bietet es sich an, zuvor eine Simulation zu erstellen. Hierzu kann eine Software wie Logisim verwendet werden. Auf diese Weise kann Zeit und Material gespart werden. Für einfache Schaltungen wie einen 4-Bit-Volladdierer ist eine Simulation zwar nicht zwingend erforderlich, bietet jedoch einige Vorteile: In der Simulation können Lernende, die erst über wenig Wissen in Digitaltechnik verfügen, gefahrlos experimentieren ohne Angst davor haben zu müssen durch Fehler Kurzschlüsse zu erzeugen, die reale Hardwarekomponenten eventuell beschädigen können. Außerdem kann der funktionierende Schaltkreisentwurf in der Simulation leicht erweitert werden. Zur späteren Beantwortung unserer Fragestellung bietet die Simulation in Logisim (Abb. 6) außerdem erste Anhaltspunkte.
Als nächste muss dieser Schaltungsentwurf in realer Hardware aufgebaut werden. Hierzu werden integrierte Logikschaltkreise der TTL-Familie verwendet. Damit dies möglichst schnell und fehlerfrei durchgeführt werden kann, wird die Schaltung auf Breadboard aufgebaut (vgl. Abb. 7). (So können die verwendeten Bauteile anschließend auch wieder-/weiterverwendet werden.) Die elektrischen Verbindungen werden auf einem Breadboard durch Stecken (statt zum Beispiel Löten auf einer Platine) hergestellt und können damit bei Bedarf leicht verändert werden. Bevor die Schaltung nun in TTL-Hardware implementiert werden kann, müssen einige Komponenten getestet werden, weil verschiedene integrierte Schaltkreise (ICs) auch verschiedene elektrische Charakteristika besitzen können. Diese können beispielsweise in den Spannungspegeln liegen, die als LOW- oder HIGH-Signale interpretiert werden. Ebenso können die Versorgungsspannung der ICs voneinander abweichen und die Schaltgeschwindigkeiten der Bauteile, die benötigt werden, um zwischen zwei Signalzuständen zu wechseln, können unterschiedlich lang sein. Insbesondere letzteres wäre für zeitkritische Anwendungen wichtig zu berücksichtigen; bei unserer Anwendung kann es allerdings vernachlässig werden. Sämtliche genannten Charakteristika lassen sich den Datenblättern der Schaltkreishersteller entnehmen.
Abbildung 7: 4-Bit-Volladdierer auf einem Breadboard
 |
 |
 |
Für unseren 4-Bit-Volladdierer werden Komponenten der 74LS-Serie (Low-Power-Schottky) verwendet. Weil in einem IC-Baustein immer mehrere Logikgatter integriert sind, kann unsere Schaltung aus drei ICs ausgebaut werden: 74LS08 (AND), 74LS86 (XOR) and 74LS32 (OR). Welche Anschlusspins miteinander verbunden werden müssen, lässt sich unserem Schaltbild (Abb. 6) sowie den Datenblättern des jeweiligen Bausteins entnehmen.
Dem Connection Diagram (Abb. 8) lassen sich die in dem Baustein enthaltenen Logik-Schaltkreise entnehmen. Sie werden durch die amerikanischen Darstellungen für Logik-Gatter repräsentiert. Die Eingänge und Ausgänge der jeweiligen Gatter lassen sich auf dem Breadboard mittels isolierter Kabel untereinander verbinden. Jede Linie auf dem Schaltdiagramm (Abb. 6) wird dabei durch eine Kabelverbindung repräsentiert. Allerdings reicht es noch nicht aus, bloß die Logikgatter untereinander zu verbinden, um die Hardware-Schaltung betreiben zu können. Zusätzlich müssen hier noch weitere Anschlüsse verkabelt werden – etwa diejenigen für die Versorgungsspannungen. Angesichts der Menge an Kabeln, die dadurch auf dem Breadboard gesteckt werden müssen, wird die Schaltung schnell unübersichtlich. Die Signalpfade können daher ebenso gut in der Simulation verfolgt werden – ein weiterer Vorteil dieser Methode.
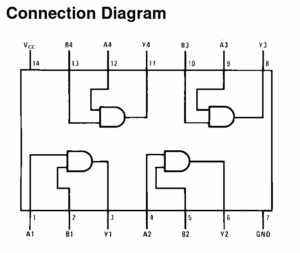
Abbildung 8: Pinout des 74LS08-IC (4-fach-AND)33
Während des ersten Tests unseres 4-Bit-Volladdierers wurde ein Fehler entdeckt: Das Ergebnis der Addition war selbst auf dem Höchstwert, wenn gar kein Eingangssignal vorlag. Dies änderte sich auch durch Änderung der Eingangswerte nicht und deutet auf einen möglichen Anschlussfehler der ICs hin. Ein solcher Fehler kann allein durch die Prüfung aller Verdrahtungen identifiziert werden, wozu Messinstrumente wie ein Digitalmultimeter oder ein Oszilloskop benötig werden. Auch die Fehlersuche gestaltet sich in der Simulation deutlich unaufwändiger, weil hier keine Messinstrumente benötigt werden; aktive Leitungen werden zum Beispiel in Logisim als ‚leuchtend‘ dargestellt.
Allein mit Hilfe eines Messinstrumentes konnte der Fehler in der Hardware-Schaltung identifiziert werden: Dieses zeigte, dass ein HIGH-Pegel an jedem Eingang des Volladdierers anlag, sobald der Eingang ‚offen‘ – also unverbunden zu einer Signalquelle – war. Um dieses Problem zu lösen, wird ein so genannter Pull-Down-Widerstand an den Eingängen benötigt, der diese mit einem definierten Statuswert versorgt. In einer Simulation wie Logisim müssen solche Besonderheiten, die auf einer Hardwareschaltung zu Problemen und Fehlfunktionen der gesamten Schaltung führen könnten, nicht berücksichtigt werden. Solche elektrotechnischen Eigenheiten finden sich in unserem Schaltungsdiagramm nicht dokumentiert, müssen beim Bau der Schaltung jedoch bedacht werden.
Der 4-Bit-Volladdierer in Minecraft
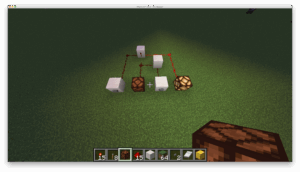
Als nächstes soll die Schaltung des 4-Bit-Volladdierers in Minecraft übertragen werden. Hierbei muss jedes einzelne Logikgatter einzeln aufgebaut werden, denn im Gegensatz zur TTL-Technik gibt es in Minecraft keine vorgefertigten Komponenten; alles muss mit Hilfe von Blöcken und Redstone-Elementen konstruiert werden. Wie oben beschrieben, gibt es oft mehrere Möglichkeiten ein Logikgatter in Minecraft zu konstruieren. Beispielweise kann ein XOR-Gatter mit deutlich weniger Blöcken und Redstone-Fackeln aufgebaut werden wie in Abb. 9 gezeigt. Die unterschiedlichen Konstruktionsmöglichkeiten sind im Minecraft-Wiki und auf anderen Webseiten gut dokumentiert.
Abbildung 9: Zwei mögliche Wege ein XOR-Gatter in Minecraft zu implementieren

Bereits zu Beginn der Aufbauarbeiten in Minecraft wurde das Ziel festgelegt, die Positionen der Logikgatter und Signalleitungen homolog zum Schaltungsdiagramm aus Abb. 6 anzulegen. Dies hat bereits ein erstes Problem erzeugt, weil sich hierbei Leitungen kreuzen würden, was durch die Konstruktion einer ‚Brücke‘, über die das Redstone-Pulver verlegt werden kann, vermieden werden konnte. Um Redstone-Leitungen voneinander zu isolieren, müssen diese mindestens zwei Blöcke voneinander entfernt verlegt werden, wie in Abb. 9 zu sehen ist. Dieselbe Problematik besteht auch auf gedruckten Schaltungen (Platinen), bei denen zwei Leitungen ebenfalls räumlich voneinander getrennt werden müssen, um voneinander isoliert zu sein.
Abbildung 10: Isolierung zweier Leitungen mittels eines Redstone-Verstärkers

Um also einen Kurzschluss der Redstone-Leitungen zu vermeiden und weil die Logikgatter in Minecraft eine bestimmte Größe besitzen, bestand ein weiteres Ziel darin, die Konstruktion des Volladdierers so kompakt wie möglich zu gestalten. Deshalb wurde eine zweite Ebene gebaut, auf dem die Hälfte der Logikgatter und Signalleitungen untergebracht wurden. Dadurch wurde die Gesamtschaltung deutlich kleiner, weil nun die Signale auch auf den unterschiedlichen Layern entlanglaufen konnten, ohne einander zu kreuzen. (Dieses Designprinzip findet sich in gleicher Funktion auch auf so genannten ‚Multi-Layer‘-Schaltungen in realer Hardware.) Die Länge der Redstone-Leitungen wurde dadurch allerdings auch größer, denn die Ausgänge bestimmter Logikgatter müssen ja an die Eingänge anderer zurückgeleitet werden. Die in Abb. 10 zu sehenden Redstone-Verstärker hatten neben dem ‚Brücken‘-Effekt daher noch den zusätzlichen Nutzen, den Leitungsverlust zu kompensieren – wie er auch ähnlich auf den Kupferleitungen realer Schaltungen aufträte. Solche Leitungsverluste sind in der zuvor vorgestellten TTL-Schaltung vernachlässigbar, müssen in konventionellen elektronischen Schaltungen und in Minecraft jedoch stets bedacht werden. Unter Berücksichtigung dessen konnte der übrige Teil der Volladdierer-Schaltung, wie in Abb. 6 entworfen, weiter aufgebaut werden.
Abbildung 11: Glas-Blöcke übertragen Signale nicht nach unten

Während des Schaltungsentwurfs in Minecraft wurde ein signifikanter Vorteil deutlich: Die Fehlersuche ist hier deutlich leichter als in Hardware-Schaltungen, weil auch hier keine Messinstrumente nötig sind. Der ‚Signalpfad‘ kann zu Fuß mit der Minecraft-Spielfigur abgeschritten werden, denn jedes HIGH-Signal wird durch die Leuchtintensität des Redstone-Pulvers repräsentiert. Die Verwendung transparenter Glas-Blöcke für den Aufbau der Ebenen erleichtert diese Beobachtungen ebenfalls; auf ihnen kann Redstone-Pulver verlegt und von oben und unten beobachtet werden. Die Verwendung von Glas-Blöcken stellte sich allerdings auch als mögliche Fehlerquelle heraus, denn diese übertragen das auf ihrer Oberseite entlanglaufende Signal – anders als andere Blöcke – nicht automatisch auf deren Unterseite (sie wirken als Isolatoren, vgl. Abb. 10). Dort, wo diese Isolator-Eigenschaft hinderlich war, wurden deshalb entweder andere Materialien verwendet oder das Schaltungsdesign verändert. Dies zeigt, dass die ‚Minecraft-Hardware‘ ebenfalls bestimmte Materialeigenschaften besitzt, die beim Übertragen eines Schaltungsdiagramms berücksichtigt werden müssen.
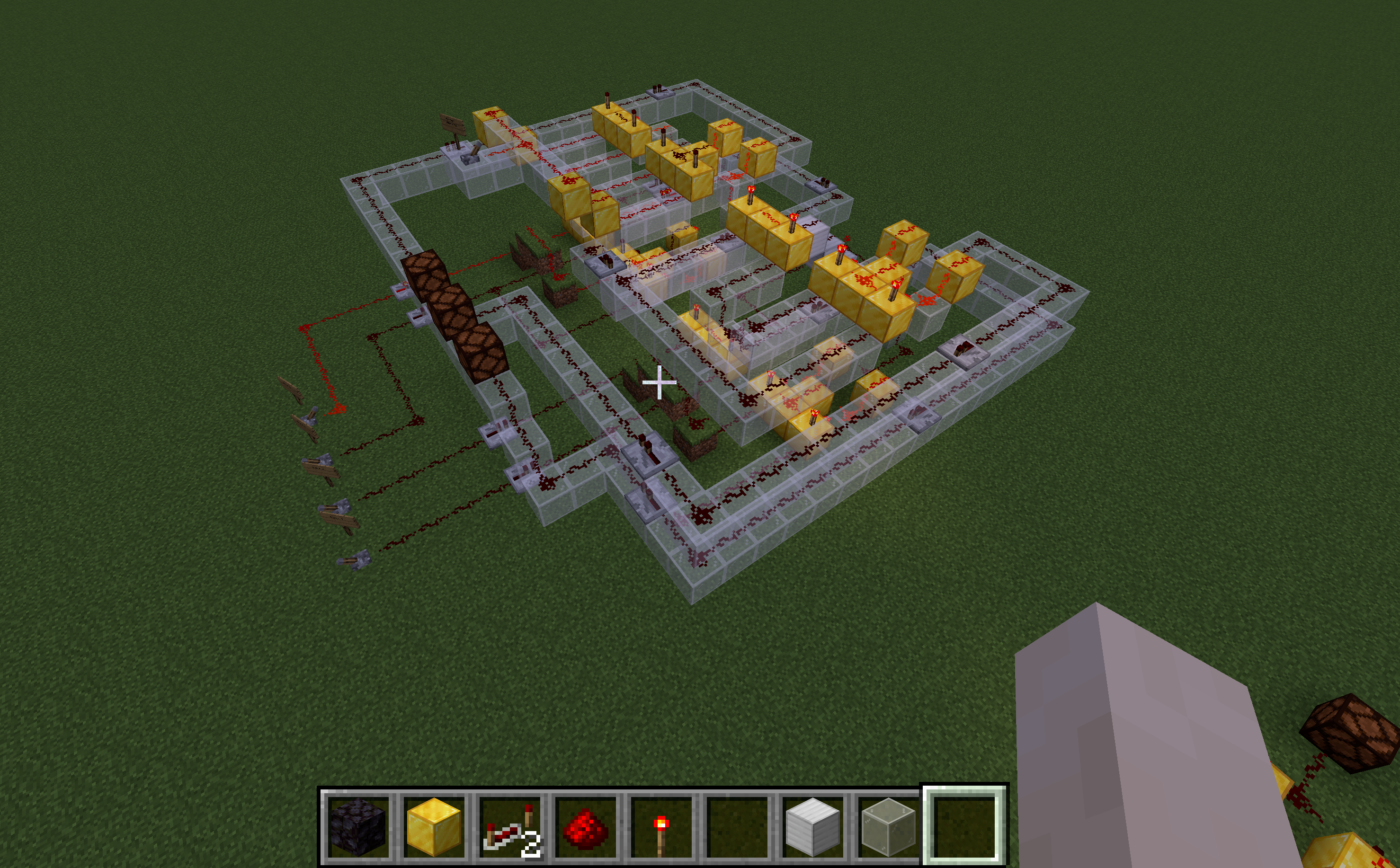
Unter Berücksichtigung solcher Spiel-spezifischer Eigenschaften konnte die Schaltung Schritt für Schritt übertragen werden. Hierbei wurden einige Möglichkeiten und Besonderheiten der Minecraft-Redstone-Technologie ergründet. Am Ende lag ein funktionsfähiger 4-Bit-Volladdierer vor, wie er in Abb. 12 zu sehen ist.
Abbildung 12: 4-Bit-Volladdierer in Minecraft
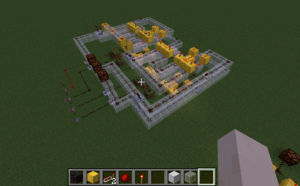
Minecraft ermöglicht es also, digitale (Computer-)Schaltkreise auf einfache Weise ‚spielerisch‘ zu konstruieren. Selbst mit nur rudimentären Kenntnissen des Spiels lassen sich Logik-Schaltkreise wie der vorgestellte 4-Bit-Volladdierer sehr schnell aufbauen. Hilfreich hierbei ist die hervorragende Dokumentation der Minecraft-Community. Allerdings sind das Wissen und die Erfahrung vom Entwurf realer Hardware-Schaltungen nicht ohne Umwege in die Minecraft-Logik übertragbar. Bei beiden bildet der theoretische Schaltungsentwurf als Diagramm den Startpunkt. Dieser dient als theoretischer Rahmen, in dem allerdings die speziellen Eigenarten des realen Schaltungstypus nicht abgebildet sind und anstelle dessen eigens bei der Konstruktion berücksichtig werden müssen. Hierzu gehören beispielsweise die verwendeten Spannungsgrößen der TTL-Gatter oder die Leitungsverluste von Redstone-Pulver-Leitungen in Minecraft.
Allerdings sind die beim Aufbau der TTL- und Minecraft-Schaltungen gefundenen Parallelen zwischen beiden Technologien ebenso interessant. Der angesprochene Signalverlust der Redstone-Leitungen oder die Isolation durch Distanzierung der Leitungen sind zwei gute Beispiele hierfür. Es zeigen sich allerdings auch Ähnlichkeiten zwischen den Simulationen in Logisim und Minecraft – etwa der als leuchtende Leitungen dargestellte HIGH-Pegel. Sowohl in Minecraft als auch in Logisim ist die Anzahl der möglichen Gatter, die miteinander verschaltet werden können, prinzipiell unbegrenzt und keine zusätzliche Hardware – etwa Pull-Down-Widerstände – werden benötigt, um eine Schaltung zu konstruieren.
Der größte Vorteil – aus Sicht der Autoren – ist allerdings die ‚spielerische‘ Vorgehensweise bei der Konstruktion der Digitalschaltkreise. Das Spiel fordert förmlich zum Experimentieren mit den spezifischen Schaltungselementen auf, denn es besteht weder die Gefahr dabei Hardware-Bauteile zu beschädigen, noch entstehen dabei Materialkosten. Minecraft zeigt sich daher als probates Tool zum Verstehen, Konstruieren und Untersuchen digitaler Logikschaltungen und theoretischer Schaltbilder wie solcher in Abb. 6. Das Wissen, solch ein Schaltbild auf ein anderes System zu übertragen, kann bei der Arbeit mit anderen Designprinzipien und Substraten hilfreich sein.
Zusammenfassung
Logic gates can be built in many ways. In mechanical computers they can be constructed by gear systems. In molecular computers they can be represented chemically. You can even use Lego toys to build (as crude and as unworkable as they are awesome) gates. Dominoes even make for a fun gate implementation (albeit one that can only be run once.)34
Dieses Grundprinzip physikalischer Objekte, sobald man sie als diskrete, binäre Schalter „missbraucht“35 ermöglicht die Implementierung von Schaltungen in zahlreichen eigentlich nicht dafür vorgesehenen Systemen. Jedes Experimentieren in dieser Richtung definiert solche Systeme neu als ‚Spielzeuge‘ und rückt sie in neue epistemische Zusammenhänge. Die Kreativität, die sich bereits bei der Idee der Umnutzung zeigt, eskaliert im Versuch, die Komplexitäten der digitalen Signalverarbeitung in die neue Umgebung zu implementieren. Hierbei stellen sich spezifische Didaktiken (‚learning by doing‘, ‚trial and error‘, Transferleistung) ein. Das konnte am Beispiel der unkonventionellen Computing-Toys im vorangegangenen Beitrag gezeigt werden.
Die spielerische Umnutzung lässt sich darüber hinaus als ein ‚Gamification‘-Prozess der (technischen) Informatik-Ausbildung verstehen, bei dem über das interaktive Spielsystem über das falsche und richtige Funktionieren der intendierten Schaltungen ein direktes Feedback die Lernenden gibt. Im Sinne klassischer Gamification-Prozesse lässt sich dies noch dadurch erweitern und forcieren, dass mehrere Lernende (über ein Netzwerk) in ein und derselben Minecraft-Welt an einem oder mehreren Projekten gleichzeitig arbeiten können und so auch größere digitale Schaltungen (bis hin zu vollständigen Computern) realisieren. Die Tatsache, dass das Spiel Minecraft als zellulärer Automat selbst ein turingvollständiges System ist, das damit jedes andere System gleicher Komplexität simulieren kann36, ermöglicht es ‚Toy Computing‘ auch, im Rahmen von Komplexitätstheorien innerhalb der theoretischen Informatik und ihrer Didaktik zu diskutieren.
Abbildungen:
Alle Abbildungen: Stefan Höltgen & Thomas Fecker
Literatur
O.A.: 74LS08 Quad 2-Input AND Gates. <http://www.sycelectronica.com.ar/semiconductores/74LS08.pdf> [10.04.2025].
O.A.: Hopper. <https://minecraft.gamepedia.com/Hopper> [10.04.2025].
O.A.: Hyperlink <https://en.wikipedia.org/wiki/Unconventional_computing> [06.06.2025].
O.A.: Minecraft Wiki. <https://minecraft-de.gamepedia.com/Minecraft_Wiki> [10.04.2025].
O.A.: Planet Minecraft Community. <https://www.planetminecraft.com/> [10.04.2025].
O.A.: Redstone circuits/Piston. <https://minecraft.fandom.com/wiki/Redstone_circuits/Piston#Piston_Gate_Designs> [10.04.2025].
O.A.: Toy Computing: Hardware-Design in „Minecraft". <https://bit.ly/3dGB7DH> [06.06.2025].
Aaronson, Scott: The Power of the Digi-Comp II / My First Conscious Paperlet. 2020. <https://www.scottaaronson.com/blog/?p=1902> [10.04.2025].
Adamatzky, Andrew (Hg.): Collision-Based Computing. London: Springer 2002.
Bouton, Charles L.: Nim, A Game with a Complete Mathematical Theory. In: The Annals of Mathematics, 2nd Ser., 1/4 (3) 1901, S. 35–39.
Cateté, V./Wassell, K./Barnes, T.: Use and Development of Entertainment Technologies in After School STEM Program. In: J. D. Dougherty/Kris Nagel (Hg.): Proceedings of the 45th ACM Technical Symposium on Computer Science Education. New York: Association for Computing Machinery 2014, S. 163–168.
Cordeiro, Jacob: Minecraft Redstone for Dummies. Hoboken: Wiley & Sons 2015.
Dezuanni, Michael : Minecraft and children’s digital making: implications for media literacy education. In: Learning, Media And Technology, 43 (3) 2018, S. 236–249.
E.S.R.: How to Play Dr. NIM. Montclair: E.S.R. Inc 1966.
E.S.R.: DIGI-COMP II. Mechanical Binary Digital Computer. Instruction Manual. Montclair: E.S.R. Inc 1967.
Frank, Helmar/Meier, Ingeborg: Rechnerkunde. Elemente der digitalen Nachrichtenverarbeitung und ihrer Fachdidaktik. Stuttgart et al.: Kohlhammer 1972.
Ekaputra, Glenn/Lim, Charles/Kho, Eng I.: Minecraft: A Game as an Education and Scientific Learning Tool. In: Information Systems International Conference (ISICO), 2 – 4 December 2013, S. 237–242.
Gobbert, Moritz: Edge Hop. Ein Modell zur Komplexitätsanalyse von kombinatorischen Spielen. MA-Arbeit 2015. <https://www.uni-trier.de/fileadmin/fb4/prof/INF/TIN/Veroeffentlichungen/Gob2015.pdf> [10.04.2025].
Heidegger, Martin: Sein und Zeit. Tübingen: Niemeyer 1967.
Heinz Nixdorf MuseumsForum: Rechenmaschine mit Kügelchen. In: HNF-Blog. Neues von gestern aus der Computergeschichte, 19. Februar 2021. <https://blog.hnf.de/rechenmaschine-mit-kuegelchen/> [05.08.2025].
Höltgen, Stefan: Computerspiele (Computer(Spiele)) – Referenzen, Zitate und Rekursionen des Computers als Spiel. In: PAIDIA, 27. Juli 2017, <https://paidia.de/computerspiele-computerspiele-referenzen-zitate-und-rekursionen-des-computers-als-spiel/> [06.06.2025].
Höltgen, Stefan: Logik. In: Ders. (Hg.): Medientechnisches Wissen, Band 1: Logik, Informations- und Speichertheorie, Archäologie. Berlin: DeGruyter/Oldenbourg 2025, S. 12–140.
Höltgen, Stefan: Open History. Archäologie der frühen Mikrocomputer und ihrer Programmierung. (Diss) 2020. <http://txt3.de/open-history> [10.04.2025].
Huhtamo, Erkki: Thinkering with Media: On The Art of Paul DeMarinis. In: Beier, Ingrid/Himmelsbach, Sabine/Seiffairth, Carsten (Hg.): Paul DeMarinis: Buried in Noise. Heidelberg/Berlin: Kehrer 2010, S. 33–46.
Hung. Patrick C. K.: Mobile Services for Toy Computing. Cham: Springer 2015.
Johnson, Matthew P.: Turing Tumble Is P(SPACE)-Complete. In: Heggernes, Pinar (Hg): Algorithms and Complexity. 11th Internationale Conference, CIAC 2019, Proceedings. Cham: Springer 2019, S. 274–285.
Kittler, Friedrich: Grammophon/Film/Typerwriter. Berlin: Brinkmann & Bose 1986.
Lane, H. C./Yi, S./Guerroro, B./Commins, N.: A Taxonomy of Minecraft Activities for STEM. In: Yang, J. C. u. a. (Hg.): Extended Summary Proceedings of the 25th International Conference on Computers in Education. New Zealand: Asia-Pacific Society for Computers in Education 2017, S. 1–3.
Mojang AB: Minecraft Education. <https://education.minecraft.net/> [10.04.2025].
Nebel, S./Schneider, S./Rey, G. D.: Mining Learning and Crafting Scientific Experiments: A Literature Review on the Use of Minecraft in Education and Research. In: Educational Technology & Society, 19 (2) 2016, S. 355–366.
Rendell, Paul: Turing Universality of the Game of Life. In: Adamatzky, Andrew (2002), a. a. O., S. 513–540.
Richardson, Craig: Learn to Program with Minecraft: Transform Your World with the Power of Python. San Francisco: No Starch Press 2015.
Rodriguez-Achach, Manuel: Make Logic Gates Out Of (Almost) Anything. <https://hackaday.com/2017/01/03/make-logic-gates-out-of-almost-anything/> [04.07.2025].
Rojas, Raúl: Konrad Zuse’s Legacy: The Architecture of the Z1 and Z3. In: IEEE Annals of the History of Computing, 19 (2) 1997, S. 5–16.
Sancarn: Proof of Concept: 100% Redstoneless Computing - Minecart Logic. <https://www.youtube.com/watch?v=qB0IuWAhd9c> [10.04.2025].
Seiffertt, John: Digital Logic for Computing. Cham: Springer 2017.
Sheffer, Henry Maurice: A Set of Five Independent Postulates for Boolean Algebras, with Application to Logical Constants. In: Transactions, American Mathematical Society 14 (1913), S. 481–88.
Turing, Alan M.: Über berechenbare Zahlen mit einer Anwendung auf das Entscheidungsproblem. In: Kittler, Friedrich A./Dotzler, Bernhard (Hg.): Alan M. Turing. Intelligence Service. Schriften. Berlin: Brinkmann & Bose 1987, S. 17–60.
Wuensche, Andrew: Finding Gliders in Cellular Automata. In: Adamatzky, Andrew (2002), a. a. O., S. 381–410.
- Vgl. O. A.: Hyperlink <https://en.wikipedia.org/wiki/Unconventional_computing> [06.06.2025].[↩]
- Vgl. Höltgen: >OPEN HISTORY_. 2020.[↩]
- Vgl. Hutamo: Thinkering. 2010.[↩]
- Vgl. Frank; Meyer: Rechnerkunde. 1972.[↩]
- Das ab Abschnitt „Digitale Logik in Minecraft“ vorgestellte Beispiel stammt von dem Studenten Thomas Fecker, dass er im Rahmen des Fachs Medienwissenschaft (BA) an der Humboldt-Universität zu Berlin im Wintersemester 2019/20 im Kurs ‚Toy Computing’ konzipiert und später umgesetzt hat (vgl. O.A.: Toy Computing: Hardware-Design in „Minecraft". <https://bit.ly/3dGB7DH> [06.06.2025].[↩]
- Vgl. Höltgen: Logik. 2025; Cordeiro: Minecraft. 2015 et al.[↩]
- O.A.: Planet Minecraft Community. <https://www.planetminecraft.com/> [10.04.2025].[↩]
- Vgl. O.A.: Minecraft Wiki. <https://minecraft-de.gamepedia.com/Minecraft_Wiki> [10.04.2025].[↩]
- Heidegger: Sein und Zeit. 1967, S. 68–72.[↩]
- Frank; Meyer: Rechnerkunde. 1972, S. 5.[↩]
- Der Begriff taucht in einer alternativen Bedeutung auf: „Toy computing incorporates the physical component of a traditional toy combined with networking and sensory capabilities of mobile devices. (…) Toy computing is a recently developing concept which transcends the traditional toy into a new area of computer research using mobile technologies.“
